ООО «НТЦ «Механотроника»
Инженер-системотехник
С.В. Михалев
Электрическая машина, тепловая защита, автоматизированные системы контроля При работе любой электрической машины выделяется тепло, представляющее собой потери энергии, которые возникают при взаимном превращении механической и электрической энергии, происходит нагрев отдельных частей электрической машины. Чрезмерное повышение температуры может вызывать в электрических машинах снижение электрической и механической прочности изоляции обмоток. Допустимая предельная температура определяется классом нагревостойкости изоляции обмоток. [1]
Целью применения тепловой защиты двигателей является исключение возможности их перегрева и, соответственно, снижения срока службы или выхода из строя.
В соответствии с «Правилами устройства электроустановок» защита от перегрузки должна предусматриваться на электродвигателях:
Защиту от перегрузки следует предусматривать в одной фазе с зависимой или независимой от тока выдержкой времени, отстроенной от длительности пуска электродвигателя в нормальных условиях и самозапуска после действия АВР и АПВ. Выдержка времени защиты от перегрузки синхронных электродвигателей во избежание излишних срабатываний при длительной форсировке возбуждения должна быть по возможности близкой к наибольшей допустимой по тепловой характеристике электродвигателя.
На электродвигателях, подверженных перегрузке по технологическим причинам, защита, как правило, должна выполняться с действием на сигнал и автоматическую разгрузку механизма.
Действие защиты на отключение электродвигателя допускается:
Для электродвигателей, которые защищаются от токов КЗ предохранителями, не имеющими вспомогательных контактов для сигнализации об их перегорании, должна предусматриваться защита от перегрузки в двух фазах.
На электродвигателях, имеющих принудительную вентиляцию, следует устанавливать защиту, действующую на сигнал и отключение электродвигателя при повышении температуры или прекращении действия вентиляции.
Отметим, что действующая в настоящее время глава 5.3 «ПУЭ» была принята ещё в 1975 г., и при её составлении, видимо, руководствовались максимальным упрощением схемы защиты в связи с тем, что двигатель является массовым потребителем электроэнергии, применение дорогих и сложных схем защиты для которого нецелесообразно. В настоящее время, в связи с широким распространением микропроцессорных средств защиты, появилась возможность реализовывать более сложные алгоритмы защиты с сохранением базовой стоимости устройства. В соответствии с этим, защита от перегрузки двигателя, устанавливаемая в одной фазе в настоящее время, как правило, не используется, защиты строятся на основе перегрузочных характеристик двигателей с учетом влияния токов обратной последовательности, предыдущего нагрева и т.п., при этом тепловые защиты устанавливаются не только на двигатели подверженные технологическим перегрузкам, но на все двигатели, поскольку превышение температуры может являться не только следствием технологической перегрузки, но и следствием, например, затянутого пуска при недопустимом моменте на валу машины и т.п.
В настоящее время распространены следующие варианты исполнения тепловой защиты:
Последний вариант исполнения защиты на первый взгляд кажется наиболее правильным и точным, к тому же высоковольтные электродвигатели часто выполняются со встроенными датчиками температуры. Однако, следует отметить, что такая мера защиты, эффективная для низковольтных электродвигателей, часто оказывается менее эффективной для высоковольтных ввиду большой толщины изоляции и массы железа а, следовательно, и гораздо больших постоянных времени нагрева и охлаждения.
Наиболее распространенным в настоящее время является вариант исполнения тепловой защиты в виде защиты от симметричных перегрузок. Объясняется это следующими её достоинствами:
Действительно данный вариант исполнения защиты прост и понятен как проектировщикам, занимающимся расчетом уставок, так и эксплуатационному персоналу. Существенным его недостатком является отсутствие учета нагрева от тока обратной последовательности, предыдущего нагрева и охлаждения электродвигателя, а также отсутствие ограничений по возможному перегреву ротора.
Защита, как правило, выполняется с обратнозависимой выдержкой времени соответствующей перегрузочной характеристике двигателя.
Указанные недостатки защиты от симметричных перегрузок успешно устраняются применением тепловой защиты на базе тепловой модели двигателя. Тепловая модель предназначена для моделирования процессов нагревания и охлаждения двигателя.
Вследствие сложности описания процессов нагревания и охлаждения различных частей электродвигателя, при разработке тепловых моделей двигателей, принимаются, как правило, следующие допущения (классическая теория нагревания [1], [2]):
Моделирование нагрева двигателя в тепловых моделях, основанных на этих допущениях, осуществляется в соответствии с дифференциальным уравнением, выражающим баланс энергии электрической машины за время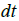 
[3]:
где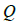 
– общее количество тепла, выделяемое в электрической машине в единицу времени 
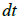(Дж/сек); 
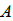– теплоотдача электрической машины, т.е. количество тепла, выделяемое ею в окружающую среду в единицу времени при разности температур в 1° (Дж/сек*град); 
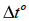- превышение температуры машины над температурой окружающей среды, выраженное в градусах; 
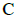– теплоемкость электрической машины, т.е. количество тепла, необходимое для повышения её температуры на 1° (Дж/град).
Принимая во внимание, что количество выделяемого в двигателе тепла пропорционально квадрату тока, запишем уравнение (1) в виде:
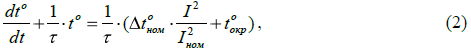
где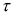 
- постоянная времени нагревания или охлаждения двигателя;
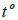- текущая температура объекта;
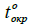- температура окружающей среды;
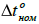- температурный перегрев объекта при номинальной мощности;
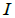- текущий ток двигателя;
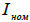- номинальный ток двигателя.
Как правило, при создании тепловых моделей в настоящее время пользуются не решением дифференциального уравнения (2) при постоянном значении тока, а общим численным решением этого уравнения, описывающим любые изменения тока.
Численное решение уравнения (2) определяется выражением (3):
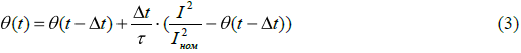
, где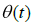 
- превышение температуры в момент времени 
.
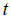Пример реализации тепловой защиты двигателя на базе уравнения (3) представлен на рисунке 1.
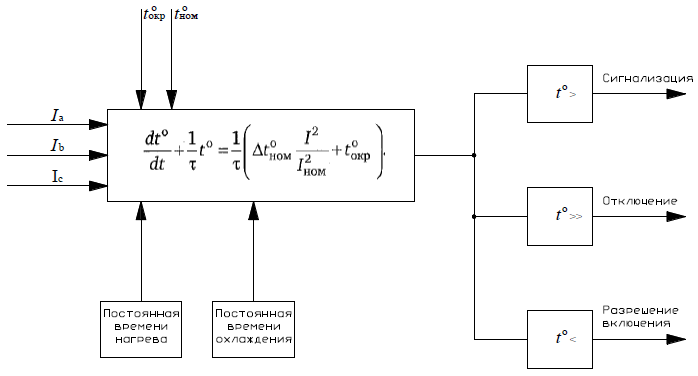
Отметим некоторые особенности такого способа реализации тепловой защиты:
В соответствии с вышесказанным, в настоящее время следует рекомендовать защиту на основе тепловой модели двигателя только при экспериментальном определении постоянных времени нагрева и охлаждения, при этом действие такой защиты осуществлять на сигнализацию. Требуется проведение дополнительных исследований по расчету и экспериментальной проверке уставок для подобного исполнения тепловой защиты.
Следует также отметить, что делались неоднократные попытки разработки методик определения постоянных времени нагрева и охлаждения электродвигателя по его паспортным данным. Однако экспериментальная проверка указанных методик проведенная сотрудниками ООО «НТЦ «Механотроника» показывает, что получаемая в результате тепловая модель дает результаты, отличающиеся от реальной температуры двигателя.
Сравним, например, результаты, получаемые с помощью рассчитанной по паспортным данным тепловой модели с результатами, полученными на физической модели.
В качестве физической модели был использован асинхронный трехфазный электродвигатель с короткозамкнутым ротором АИР100S4 мощностью 3кВт. В качестве датчиков температуры использовались два терморезистора типа ММТ-1, один из которых был механически прикреплен снаружи к корпусу двигателя, а второй встроен в лобовую часть обмоток внутри корпуса.
Анализ тепловых параметров математической модели проводился для следующих режимов:
-пуск и стационарная длительная работа при номинальном напряжении питания с нагрузкой 1,2 номинальной при температуре окружающей среды минус 20оС до срабатывания защиты или в течении 0,3 часа;
-пуск и работа в повторно-кратковременном режиме с ПВ-40% и продолжительностью цикла ПВ 0,2 часа при номинальном напряжении питания с нагрузкой 1,2 номинальной при температуре окружающей среды минус 20оС до срабатывания защиты или в течении одного часа.
При проведении эксперимента использовалась тепловая модель, рассчитывающая относительный перегрев двигателя, где за 100% принято значение перегрева двигателя при длительной работе с номинальной нагрузкой.
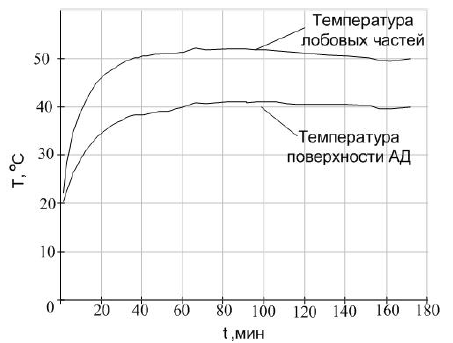
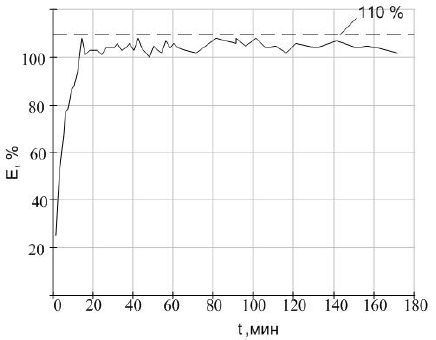
Из результатов проведенного эксперимента следует, что тепловая модель соответствует реальному электродвигателю только в очень грубом приближении. Так во время эксперимента температура нагрева лобовых частей достигла 52°С, а по данным модели относительный перегрев составил более 100%. Простой расчет показывает, что относительный перегрев в 120% при котором защита отключает двигатель будет соответствовать 62,4°С, что значительно меньше допустимой температуры нагрева изоляции 105°С. Поэтому использование такой модели не позволяет полностью использовать перегрузочную способность защищаемого электродвигателя. Результаты измерения температуры лобовых частей и поверхности асинхронного двигателя приведены на рисунке 2. Результаты работы тепловой модели приведены на рисунке 3.
На основании приведенных выше данных можно сделать вывод: используемые в настоящее время тепловые модели могут адекватно отражать процесс нагрева электродвигателей только при предварительном определении постоянных времени нагрева и охлаждения экспериментальным методом, что не всегда осуществляется при проведении пуско-наладочных работ. Вследствие этого, в настоящее время, перспективными темами научных работ могут являться: корректное определение постоянных времени нагрева и охлаждения электродвигателя на основе его паспортных данных, а также разработка тепловых моделей двигателя не требующих задания экспериментально-определяемых параметров. В рамках данного доклада предлагается несколько возможных путей разработки подобных тепловых моделей.
Из методики испытаний электродвигателей, приведенной в ГОСТ 7217-87 [4] известен метод определения температуры обмотки статора по её электрическому сопротивлению. Полное сопротивление двигателя может быть определено в процессе его работы, из него можно получить активное и реактивное сопротивление двигателя. Проведя расчет активных и индуктивных сопротивлений обмоток двигателя в соответствии с методикой, приведенной в [5], получаем параметры эквивалентной Т-образной схемы замещения асинхронного электродвигателя (см. рис. 4).
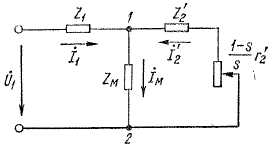
По данной схеме определяем полное сопротивление электродвигателя Z. Рассмотрим влияние величины скольжения (нагрузки) электродвигателя на активную и реактивную составляющие Z (см. рис. 5)
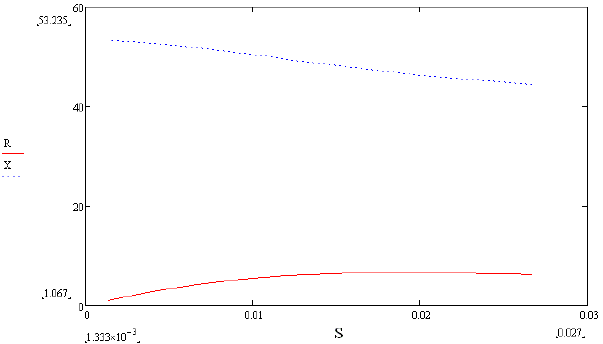
Из полученной зависимости реактивного сопротивления двигателя от величины скольжения может быть определено текущее скольжение электродвигателя в зависимости от текущего значения его реактивного сопротивления. В свою очередь из полученной величины скольжения может быть определено текущее значение активной составляющей сопротивления. Разница между измеренным значением активного сопротивления и значением, полученным из характеристики (рис. 4) и составляет то изменение сопротивления, которое обусловлено изменением температуры обмотки. Однако несложный расчет показывает, что при изменении температуры медной обмотки на 100К сопротивление обмотки увеличится на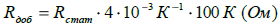 
, где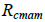 
– сопротивление статора холодного двигателя. При типовых значениях активного сопротивления статора 0,5 Ом, получаем значение 
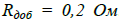. Таким образом, для определения температуры двигателя с точностью 5К требуется измерение активного сопротивления статора «на ходу» с точностью 0,01 Ом, что в настоящее время недостижимо. Тем не менее, подход может стать актуальным при дальнейшем развитии средств измерения тока и напряжения, например переходе к оптическим трансформаторам. Для измерения активного сопротивления обмотки статора может использоваться наложение на питающее напряжение сигналов, например постоянного тока или импульсов низкой частоты, и дальнейшее измерение активного сопротивления обмотки относительно наложенных сигналов. Подобный подход может быть также интересен с точки зрения создания автоматизированной системы оценки состояния обмоток статора.
Другой альтернативой использующимся в настоящее время упрощенным однокорпусным моделям может служить модель, предполагающая представление двигателя в виде совокупности однородных тел (напр. обмотки ротора, активной стали ротора, активной стали статора, обмотки статора, корпуса двигателя). Теория теплообмена для такого представления хорошо разработана в теории проектирования электрических машин (см. [3]), а современные процессоры и контроллеры позволяют реализовать расчет таких моделей в реальном времени.
Рассмотрим для примера тепловую схему замещения статора асинхронной машины, представленную на рисунке 6.
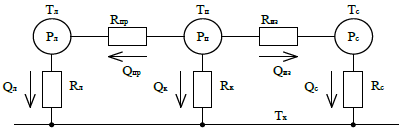
В представленной модели: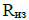 
– тепловое сопротивление пазовой изоляции, 
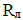– тепловое сопротивление лобовой части обмотки, 
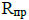– тепловое сопротивление металла всех стержней обмотки по длине проводника, 
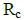– тепловое сопротивление магнитопровода охлаждающему воздуху, 
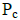– потери сердечника, 
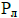– суммарные потери лобовых частей обмотки, 
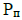– потери пазовой части обмотки. При расчете динамики нагрева должна быть учтена также теплоемкость каждой из зон, на которую подразделяется электрическая машина. Для вычисления динамики нагрева частей электрической машины в соответствии с данной моделью требуется решение системы из 3 дифференциальных уравнений:
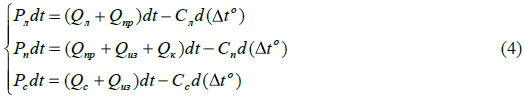
, где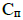 
– теплоемкость пазовой части обмотки статора, 
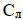– теплоемкость лобовых частей обмотки статора, 
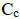– теплоемкость активной стали статора.
Сложность практической реализации подобной модели заключается, конечно, не в недостатке вычислительных ресурсов, а в сложности определения входящих в уравнение коэффициентов: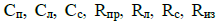 
. Для расчета указанных коэффициентов, как правило, требуется знание множества конструктивных параметров электрической машины неизвестных инженеру, осуществляющему настройку электропривода или системы защиты двигателя.
В целом задачу можно сформулировать следующим образом:
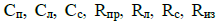.Разработка многокорпусной тепловой модели электрической машины, а также определение её параметров также являются в настоящее время перспективными задачами научной работы.
Рассмотрим ещё один подход к созданию тепловой модели двигателя. Поскольку мы обладаем некоторыми ориентировочными знаниями о структуре тепловой модели и диапазонах значений её параметров, но с другой стороны точные значения параметров и точная структура модели для данной конкретной машины нам неизвестны, возможен подход к решению подобной задачи на базе теории нейронных сетей. Изучение источников [6], [7] показывает, что решение поставленной задачи возможно путем создания многослойной нейронной сети и дальнейшего её обучения. Рассмотрим, например, двухслойную (два скрытых слоя) нейронную сеть с обучением. Для предварительного обучения системы предлагается использовать информацию со встроенных температурных датчиков двигателей, обеспечивающих измерение температур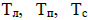 
. В качестве экспертных оценок используются знания о предполагаемой структуре модели и о возможных диапазонах изменения параметров 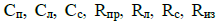для выбранного типа электрических машин. В качестве функций активации нейронов целесообразно использовать функцию, отражающую экспоненциальную зависимость, например гиперболический тангенс. Известно [6], что с помощью двухслойной нейронной сети можно получить аппроксимацию любой функции, пределы достижимой точности в этом случае будут определяться количеством нейронов в слоях. Входными параметрами нейронной сети являются значения токов двигателя выходными параметрами – значения температур 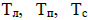. Для учета температуры, до которой нагрелась составная часть электродвигателя за прошедшее до текущего момента время необходимо использование нейронов с обратными связями. Обучение проводится с помощью алгоритма обратного распространения ошибки, при этом в качестве обучающей выборки используются данные о значении токов двигателя и данные, полученные с тепловых датчиков двигателя за некоторый интервал времени.
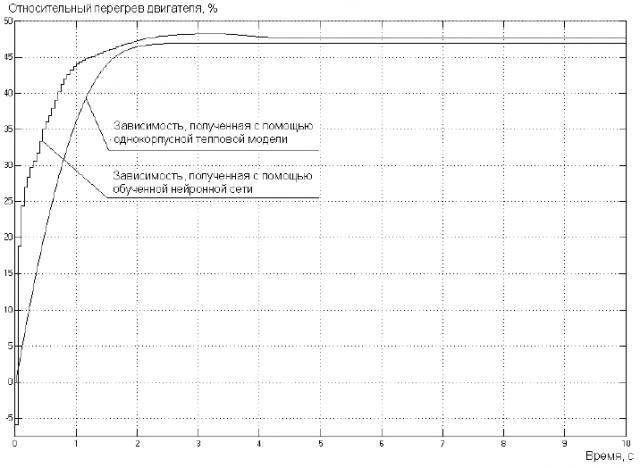
Приведу далее результаты модельного эксперимента, в котором в качестве обучающей выборки использовались данные, полученные от однокорпусной тепловой модели двигателя. Обучающая выборка получена после окончания процесса пуска двигателя. Использована двухслойная сеть Элмана с числом нейронов в первом слое: 10, во втором слое: 2. Обучение сети проводилось по методу обратного распространения ошибки. Время обучения на типовой современной ЭВМ составило 30 секунд. Результаты работы нейронной сети, в сравнении с результатами однокорпусной тепловой модели приведены на рисунке 7. Результаты получены при значении нагрузки моделируемого двигателя отличной от нагрузки, использованной при расчете обучающей выборки.
Полученные результаты доказывают принципиальную возможность создания тепловой модели двигателя на базе нейронной сети с использованием в качестве обучающей выборки экспериментальных данных о нагреве двигателя.
В заключение, укажу возможные области применения уточненных тепловых моделей двигателей:
Никто пока не комментировал эту страницу.